Details:Physics

Moisture Transport in Building Materials

Computer Simulation with the WUFI Model

Introduction

For the practitioner the subject "moisture transport in building materials" mainly evokes vapor diffusion, dew point and the Glaser method described in German standard DIN 4108. Once a building element has been classified as "safe according to Glaser", all is over and done with as far as the designer is concerned.

Only if unexpected moisture damage occurs nevertheless, or if the designed building element does not pass the standard Glaser assessment, the search for alternative assessment methods begins. Since condensation by vapor transport in winter (which is what Glaser investigates) is only one of a large number of possible moisture loads on a building element, a positive assessment according to DIN 4108 may imply moisture safety which does not really exist. Possible problems with other hygric processes, such as indoor air convection, precipitation or rising damp, are usually not considered. The same goes for construction moisture which, in view of today's deadline pressure, causes an increasing number of damage cases. In order to allow for these effects too, one has to pass on from Glaser's simple steady-state assessment method to the realistic simulation of hygric processes in building elements. To this end, new non-steady simulation methods have been developed and experimentally validated in recent years, whose reliability is winning them more and more acceptance among practitioners. This fact is also recognized in the new draft for DIN 4108-3 which now admits these methods. In the following we will demonstrate the effects of increased moisture levels and of alternating hygric stresses, and we will describe the basic physics of hygric processes in building elements. Subsequently, we will analyse the necessary climate and material data and discuss the accuracy of the calculation, using the non-steady simulation model WUFI as an example which has meanwhile found widespread use.

Hygric Effects in Building Components

The fitness for use and the durability of building components and building materials may be affected by moisture, as shown by these examples:

• reduction of thermal insulation
• increased dust contamination, algae or mold growth
• mechanical stresses through swelling and shrinking caused by changes in humidity or by salt crystallization
• damages due to frost, rotting or corrosion, caused by increased moisture in the material
• incomplete hydratation because of drying too rapidly
• delayed maturing of screed topping because of drying too slowly

Heat Losses due to moisture

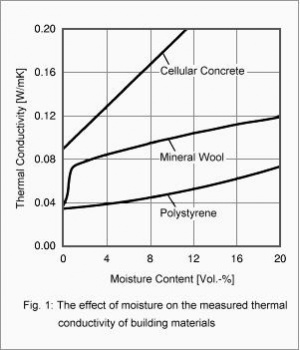
The heat and moisture transport processes in buildings are usually strongly coupled. This is particularly evident in the effect of moisture on the heat insulation of building components. Fig. 1 shows the increase in heat conductivity of three different building materials as dependent on their moisture content [1].

While the heat conductivity of mineral materials, such as the cellular concrete shown here, increases linearly with moisture content, the heat conductivity of polystyrene foam shows a slightly progressive increase. Surprisingly, it takes only a very low moisture content to increase the heat conductivity of mineral wool markedly. This is due to the pronounced moisture redistribution by vapor diffusion in the mineral wool when a temperature gradient is applied across the sample. These are so-called non-steady latent heat effects, due to phase changes of the moisture in the material during the measurement in the guarded hot plate apparatus. These latent heat effects are usually of short duration only and have nothing to do with the true heat conductivity of the insulation material. Since their effect depends strongly on the materials adjacent to the insulation layer, they are not a characteristic of the insulation material itself [2]. Therefore the heat conductivity of mineral wool determined in this way and shown in Fig. 1 is not well suited as a material property function for non-steady calculations or for determining the steady-state U-factor. The true heat conductivity of mineral wool can be determined in the guarded hot plate apparatus if appropriate precautions are employed. Results of such measurements demonstrate that if latent heat effects are excluded, the heat conductivity of mineral wool shows a moisture dependence very similar to that of the polystyrene foam in Fig. 1. Similar remarks apply to other permeable insulation materials.

Mechanical Stress due to Alternating Hygric Loads

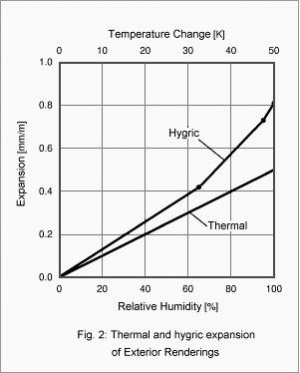
One example for the strongly non-steady character of the coupled thermal and hygric effects is the mechanical strain due to thermal and hygric expansion and the resulting internal stress in the renderings on exterior thermal insulation composite systems (ETICS). During the course of the day the surface of these renderings is exposed to thermal and hygric variations of up to 40 K and 80% RH [3]. Fig. 2 compares the thermal and hygric expansion of such exterior renderings. The shown values represent averages over laboratory measurements performed on more than 20 specimens of different manufacturers. Compared with practical conditions to which a building is exposed this means a thermal expansion of 0.4 mm/m and an even larger hygric expansion of 0.7 mm/m (if the rendering could expand freely). Both processes often partially cancel each other out, however, since increased temperature dries the rendering, so that the thermal expansion is compensated by hygric shrinking after some delay. Since the rendering surfaces usually can not move freely, any expansion results in internal stress and - if the material strength is exceeded - in cracks or in separation from the rendering base due to shear failure.

Other examples for damages caused by alternating hygrothermal strain are salt and frost damages. Below a certain relative humidity which is characteristic for a specific type of salt, salts are crystallizing out of the solution. Conversely, when this crystallization point is exceeded, they absorb ambient water vapor and dissolve again. These processes also occur in the pore spaces of building materials if these contain salts. There, however, crystallization is impeded by the narrow pore structures and considerable crystallization pressures may result, so that frequent humidity cycles can embrittle the material. Depending on the solubility of the salt, this process may occur at the surface, or several millimeters or centimeters below, and may thus lead to crumbling at the surface or to shaling due to destabilization of deeper layers [4]. Frost can cause similar types of damage, with the ice crystals acting the same way as the salt crystals. Here the decisive factors are frequent temperature variations around the freezing point and sufficient moisture in the frost zone [5].

The above examples demonstrate the effect of alternating hygrothermal strains on the durability and the fitness for use of building components and building materials. Therefore it is not only desirable but absolutely essential to determine precisely the thermal and hygric processes occurring in these. Assessments using the traditional methods which are exclusively based on vapor diffusion (such as the Glaser method) can achieve this in exceptional cases only. However, computer simulations of non-steady thermal and hygric processes, including all essential transport mechanisms under natural climate conditions have meanwhile been developed to maturity and have proven successful in practice, so that their systematic application in many areas of building construction appears useful. The discussion which follows is to be understood in this context.

Moisture Storage and Transport Mechanisms

The successful application of simulation models for non-steady thermal and hygric processes in building components requires some basic knowledge about the storage and transport properties of building materials. Since heat storage and thermal conduction are well known and heat transport by vapor diffusion with phase change (latent heat effect) is to be treated in the context of moisture transport, the following discussion only deals with hygric phenomena. For a detailed analysis of frost-dew cycles which are determined by the latent heat of fusion and the thermal properties of ice, please refer to [2].

Moisture Storage

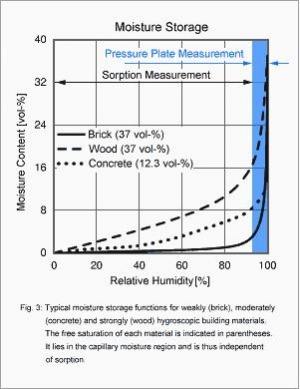
There are hygroscopic and non-hygroscopic building materials. If a material is hygroscopic, then an initially dry sample will absorb moisture from the air until it reaches its equilibrium moisture corresponding to the ambient conditions. Since water vapor absorption mainly depends on the ambient relative humidity whereas the ambient temperature has less influence, the hygroscopic moisture storage is described by means of material-specific sorption curves.

Fig. 3 shows such sorption curves (also known as sorption isotherms) for three building materials which differ markedly in their hygroscopicity. The sorption isotherms are determined by exposing the samples to different ambient conditions in the laboratory until equilibrium is reached. The highest reachable relative humidity is ca. 95% since in most climate chambers the climate control is not fine enough to reliably avoid moisture condensing on the samples at higher humidities. Above this RH and up to free water saturation, i.e. in the so-called capillary water region, measurements must therefore be performed with the pressure plate apparatus described in [6]. For this method material samples are first kept submerged in water until free (i.e. with no pressure applied) saturation is reached. Then the samples are exposed to a series of different barometric pressure levels up to 100 bar. At each level, some water is forced out of the specimen until equilibrium is reached for this pressure. Analysis of the measurement results in a capillary moisture storage function (in the blue region of Fig. 3), which smoothly continues the classical sorption isotherm. In building materials with coarse pores, such as brick, the capillary water region is larger than the hygroscopic region, so that pressure plate measurements are indispensable for detailed analyses. In materials with fine pores, such as concrete, the sorption moisture content at 93% RH is already so high that the sorption isotherm can be extrapolated into the capillary water region and up to free saturation without loss of accuracy. Wood and processed wood materials, too, already absorb large quantities of moisture in the hygroscopic region, so that in these cases extrapolation up to free saturation is usually sufficient as well.

In non-hygroscopic materials, for example glass, metal or some plastic foams, no water accumulates unless the temperature falls below the dew point. Under ambient conditions below 100% RH they dry out completely.

Moisture Transport

In porous building materials the predominant moisture transport mechanisms are vapor diffusion, surface diffusion and capillary conduction. In materials which do not have a rigid pore structure, for example plastics, so-called solution diffusion occurs because water molecules squeeze between the polymeric macromolecules. Experience shows that this kind of diffusion can best be described by the laws governing vapor diffusion, with a diffusion resistance factor which is now dependent on ambient humidity (in contrast to normal vapor diffusion where the diffusion resistance is independent of humidity).

Other transport phenomena, for example seepage flow through gravitation in non-saturated pore spaces or migration of water molecules due to electric fields or osmotic pressures, cannot yet be computed in a satisfactory way. However, since they only play a major part in exceptional cases, they are not further considered here. Convection effects, for example moist interior air permeating building components because of pressure differentials between the interior and the exterior side, are ignored as well. Since airtightness is an essential property of a building wall, air convection is in practice only found in unplanned cases of defective parts or inappropriate building components. It is therefore difficult to quantify beforehand and could also only be realistically determined by three-dimensional fluid dynamical simulation programs.

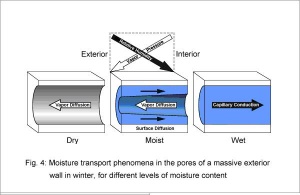
The combined effect of the abovementioned predominant moisture transport mechanisms is illustrated in Fig. 4, using a cylindrical capillary in a building material as an example. On both sides of the capillary typical boundary conditions are assumed as they are usually encountered in practice, i.e. the vapor pressure is greater on the interior side and the relative humidity is greater on the exterior side. If the material is sufficiently dry or not hygroscopic, then the water vapour will diffuse from inside to outside, following the direction from higher to lower vapor pressure.

If the material contains enough hygroscopic moisture, so that the sorbate film on the pore walls becomes mobile (this happens at humidities above ca. 60%), then we find so-called surface diffusion due to sorbed water on the pore walls superimposed on the normal vapor diffusion in the pore air. Since the thickness and therefore the mobility of the sorbed molecular layer increases with relative humidity, moisture transport in the sorbate film results, following the direction from regions with higher concentration to regions with lower concentration of sorbed water, as demonstrated in [6]. The driving force for surface diffusion is therefore relative humidity and not vapor pressure. Thus under the boundary conditions assumed here, vapor diffusion and surface diffusion go in opposite directions. Surface diffusion must therefore be regarded as a type of liquid transport, not a type of vapor transport in the gas phase. Nevertheless, it may often be practical to combine surface diffusion with vapor diffusion, for example by employing the µ-factor determined in a wet-cup test according to DIN 52615. This procedure yields similar calculation results as a strict distinction between the two transport phenomena, as long as no major temperature gradients occur in the investigated material layer.

Under capillary moisture conditions in the material, for example due to driving rain, the capillaries start to fill up and capillary conduction sets in, the most efficient type of moisture transport. Here the driving force is the capillary tension which results from the surface tension of the water in the meniscus at the interface between water and pore air. There exists a functional relation between the capillary tension and the equilibrium humidity in the pore air above the meniscus, i.e. the driving force in the liquid phase corresponds to a certain relative humidity in the gas phase. Thus instead of capillary tension, relative humidity can be used as driving potential for capillary conduction.

As the example shows clearly, the transport directions of vapor diffusion and liquid transport may often be opposed to each other. Vapor diffusion usually occurs from warm to cold, whereas liquid transport goes from moist to dry, mostly independent of temperature. This phenomenon, presumably known to each practitioner who has ever observed how condensed moisture in winter can be drawn off by mineral materials, must be correctly included in a simulation model, in accordance with the above analysis. This means that different driving forces must be employed for vapor diffusion and liquid transport. The choice of temperature and relative humidity as driving potentials offers particular advantages. Vapor pressure, as the driving force for diffusion, is uniquely determined by the two quantities. The two potentials are continuous across the building component, i.e. there are no discontinuities at material interfaces, as would be the case with water content. In addition, the hygrothermal material properties and boundary conditions discussed in the following can easily be defined in terms of these quantities.