Details:Physics

Moisture Transport in Building Materials

Computer Simulation with the WUFI Model

Introduction

For the practitioner the subject "moisture transport in building materials" mainly evokes vapor diffusion, dew point and the Glaser method described in German standard DIN 4108. Once a building element has been classified as "safe according to Glaser", all is over and done with as far as the designer is concerned.

Only if unexpected moisture damage occurs nevertheless, or if the designed building element does not pass the standard Glaser assessment, the search for alternative assessment methods begins. Since condensation by vapor transport in winter (which is what Glaser investigates) is only one of a large number of possible moisture loads on a building element, a positive assessment according to DIN 4108 may imply moisture safety which does not really exist. Possible problems with other hygric processes, such as indoor air convection, precipitation or rising damp, are usually not considered. The same goes for construction moisture which, in view of today's deadline pressure, causes an increasing number of damage cases. In order to allow for these effects too, one has to pass on from Glaser's simple steady-state assessment method to the realistic simulation of hygric processes in building elements. To this end, new non-steady simulation methods have been developed and experimentally validated in recent years, whose reliability is winning them more and more acceptance among practitioners. This fact is also recognized in the new draft for DIN 4108-3 which now admits these methods. In the following we will demonstrate the effects of increased moisture levels and of alternating hygric stresses, and we will describe the basic physics of hygric processes in building elements. Subsequently, we will analyse the necessary climate and material data and discuss the accuracy of the calculation, using the non-steady simulation model WUFI as an example which has meanwhile found widespread use.

Hygric Effects in Building Components

The fitness for use and the durability of building components and building materials may be affected by moisture, as shown by these examples:

• reduction of thermal insulation
• increased dust contamination, algae or mold growth
• mechanical stresses through swelling and shrinking caused by changes in humidity or by salt crystallization
• damages due to frost, rotting or corrosion, caused by increased moisture in the material
• incomplete hydratation because of drying too rapidly
• delayed maturing of screed topping because of drying too slowly

Heat Losses due to moisture

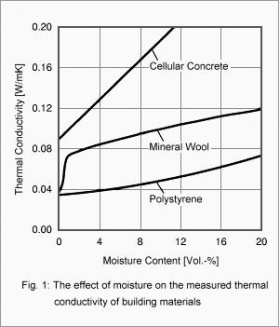
The heat and moisture transport processes in buildings are usually strongly coupled. This is particularly evident in the effect of moisture on the heat insulation of building components. Fig. 1 shows the increase in heat conductivity of three different building materials as dependent on their moisture content [1].

While the heat conductivity of mineral materials, such as the cellular concrete shown here, increases linearly with moisture content, the heat conductivity of polystyrene foam shows a slightly progressive increase. Surprisingly, it takes only a very low moisture content to increase the heat conductivity of mineral wool markedly. This is due to the pronounced moisture redistribution by vapor diffusion in the mineral wool when a temperature gradient is applied across the sample. These are so-called non-steady latent heat effects, due to phase changes of the moisture in the material during the measurement in the guarded hot plate apparatus. These latent heat effects are usually of short duration only and have nothing to do with the true heat conductivity of the insulation material. Since their effect depends strongly on the materials adjacent to the insulation layer, they are not a characteristic of the insulation material itself [2]. Therefore the heat conductivity of mineral wool determined in this way and shown in Fig. 1 is not well suited as a material property function for non-steady calculations or for determining the steady-state U-factor. The true heat conductivity of mineral wool can be determined in the guarded hot plate apparatus if appropriate precautions are employed. Results of such measurements demonstrate that if latent heat effects are excluded, the heat conductivity of mineral wool shows a moisture dependence very similar to that of the polystyrene foam in Fig. 1. Similar remarks apply to other permeable insulation materials.

Mechanical Stress due to Alternating Hygric Loads

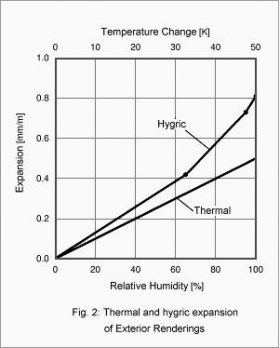
One example for the strongly non-steady character of the coupled thermal and hygric effects is the mechanical strain due to thermal and hygric expansion and the resulting internal stress in the renderings on exterior thermal insulation composite systems (ETICS). During the course of the day the surface of these renderings is exposed to thermal and hygric variations of up to 40 K and 80% RH [3]. Fig. 2 compares the thermal and hygric expansion of such exterior renderings. The shown values represent averages over laboratory measurements performed on more than 20 specimens of different manufacturers. Compared with practical conditions to which a building is exposed this means a thermal expansion of 0.4 mm/m and an even larger hygric expansion of 0.7 mm/m (if the rendering could expand freely). Both processes often partially cancel each other out, however, since increased temperature dries the rendering, so that the thermal expansion is compensated by hygric shrinking after some delay. Since the rendering surfaces usually can not move freely, any expansion results in internal stress and - if the material strength is exceeded - in cracks or in separation from the rendering base due to shear failure.

Other examples for damages caused by alternating hygrothermal strain are salt and frost damages. Below a certain relative humidity which is characteristic for a specific type of salt, salts are crystallizing out of the solution. Conversely, when this crystallization point is exceeded, they absorb ambient water vapor and dissolve again. These processes also occur in the pore spaces of building materials if these contain salts. There, however, crystallization is impeded by the narrow pore structures and considerable crystallization pressures may result, so that frequent humidity cycles can embrittle the material. Depending on the solubility of the salt, this process may occur at the surface, or several millimeters or centimeters below, and may thus lead to crumbling at the surface or to shaling due to destabilization of deeper layers [4]. Frost can cause similar types of damage, with the ice crystals acting the same way as the salt crystals. Here the decisive factors are frequent temperature variations around the freezing point and sufficient moisture in the frost zone [5].

The above examples demonstrate the effect of alternating hygrothermal strains on the durability and the fitness for use of building components and building materials. Therefore it is not only desirable but absolutely essential to determine precisely the thermal and hygric processes occurring in these. Assessments using the traditional methods which are exclusively based on vapor diffusion (such as the Glaser method) can achieve this in exceptional cases only. However, computer simulations of non-steady thermal and hygric processes, including all essential transport mechanisms under natural climate conditions have meanwhile been developed to maturity and have proven successful in practice, so that their systematic application in many areas of building construction appears useful. The discussion which follows is to be understood in this context.

Moisture Storage and Transport Mechanisms

The successful application of simulation models for non-steady thermal and hygric processes in building components requires some basic knowledge about the storage and transport properties of building materials. Since heat storage and thermal conduction are well known and heat transport by vapor diffusion with phase change (latent heat effect) is to be treated in the context of moisture transport, the following discussion only deals with hygric phenomena. For a detailed analysis of frost-dew cycles which are determined by the latent heat of fusion and the thermal properties of ice, please refer to [2].

Moisture Storage

There are hygroscopic and non-hygroscopic building materials. If a material is hygroscopic, then an initially dry sample will absorb moisture from the air until it reaches its equilibrium moisture corresponding to the ambient conditions. Since water vapor absorption mainly depends on the ambient relative humidity whereas the ambient temperature has less influence, the hygroscopic moisture storage is described by means of material-specific sorption curves.

Fig. 3 shows such sorption curves (also known as sorption isotherms) for three building materials which differ markedly in their hygroscopicity. The sorption isotherms are determined by exposing the samples to different ambient conditions in the laboratory until equilibrium is reached. The highest reachable relative humidity is ca. 95% since in most climate chambers the climate control is not fine enough to reliably avoid moisture condensing on the samples at higher humidities. Above this RH and up to free water saturation, i.e. in the so-called capillary water region, measurements must therefore be performed with the pressure plate apparatus described in [6]. For this method material samples are first kept submerged in water until free (i.e. with no pressure applied) saturation is reached. Then the samples are exposed to a series of different barometric pressure levels up to 100 bar. At each level, some water is forced out of the specimen until equilibrium is reached for this pressure. Analysis of the measurement results in a capillary moisture storage function (in the blue region of Fig. 3), which smoothly continues the classical sorption isotherm. In building materials with coarse pores, such as brick, the capillary water region is larger than the hygroscopic region, so that pressure plate measurements are indispensable for detailed analyses. In materials with fine pores, such as concrete, the sorption moisture content at 93% RH is already so high that the sorption isotherm can be extrapolated into the capillary water region and up to free saturation without loss of accuracy. Wood and processed wood materials, too, already absorb large quantities of moisture in the hygroscopic region, so that in these cases extrapolation up to free saturation is usually sufficient as well.

In non-hygroscopic materials, for example glass, metal or some plastic foams, no water accumulates unless the temperature falls below the dew point. Under ambient conditions below 100% RH they dry out completely.

Moisture Transport

In porous building materials the predominant moisture transport mechanisms are vapor diffusion, surface diffusion and capillary conduction. In materials which do not have a rigid pore structure, for example plastics, so-called solution diffusion occurs because water molecules squeeze between the polymeric macromolecules. Experience shows that this kind of diffusion can best be described by the laws governing vapor diffusion, with a diffusion resistance factor which is now dependent on ambient humidity (in contrast to normal vapor diffusion where the diffusion resistance is independent of humidity).

Other transport phenomena, for example seepage flow through gravitation in non-saturated pore spaces or migration of water molecules due to electric fields or osmotic pressures, cannot yet be computed in a satisfactory way. However, since they only play a major part in exceptional cases, they are not further considered here. Convection effects, for example moist interior air permeating building components because of pressure differentials between the interior and the exterior side, are ignored as well. Since airtightness is an essential property of a building wall, air convection is in practice only found in unplanned cases of defective parts or inappropriate building components. It is therefore difficult to quantify beforehand and could also only be realistically determined by three-dimensional fluid dynamical simulation programs.

The combined effect of the abovementioned predominant moisture transport mechanisms is illustrated in Fig. 4, using a cylindrical capillary in a building material as an example. On both sides of the capillary typical boundary conditions are assumed as they are usually encountered in practice, i.e. the vapor pressure is greater on the interior side and the relative humidity is greater on the exterior side. If the material is sufficiently dry or not hygroscopic, then the water vapour will diffuse from inside to outside, following the direction from higher to lower vapor pressure.

If the material contains enough hygroscopic moisture, so that the sorbate film on the pore walls becomes mobile (this happens at humidities above ca. 60%), then we find so-called surface diffusion due to sorbed water on the pore walls superimposed on the normal vapor diffusion in the pore air. Since the thickness and therefore the mobility of the sorbed molecular layer increases with relative humidity, moisture transport in the sorbate film results, following the direction from regions with higher concentration to regions with lower concentration of sorbed water, as demonstrated in [6]. The driving force for surface diffusion is therefore relative humidity and not vapor pressure. Thus under the boundary conditions assumed here, vapor diffusion and surface diffusion go in opposite directions. Surface diffusion must therefore be regarded as a type of liquid transport, not a type of vapor transport in the gas phase. Nevertheless, it may often be practical to combine surface diffusion with vapor diffusion, for example by employing the µ-factor determined in a wet-cup test according to DIN 52615. This procedure yields similar calculation results as a strict distinction between the two transport phenomena, as long as no major temperature gradients occur in the investigated material layer.

Under capillary moisture conditions in the material, for example due to driving rain, the capillaries start to fill up and capillary conduction sets in, the most efficient type of moisture transport. Here the driving force is the capillary tension which results from the surface tension of the water in the meniscus at the interface between water and pore air. There exists a functional relation between the capillary tension and the equilibrium humidity in the pore air above the meniscus, i.e. the driving force in the liquid phase corresponds to a certain relative humidity in the gas phase. Thus instead of capillary tension, relative humidity can be used as driving potential for capillary conduction.

As the example shows clearly, the transport directions of vapor diffusion and liquid transport may often be opposed to each other. Vapor diffusion usually occurs from warm to cold, whereas liquid transport goes from moist to dry, mostly independent of temperature. This phenomenon, presumably known to each practitioner who has ever observed how condensed moisture in winter can be drawn off by mineral materials, must be correctly included in a simulation model, in accordance with the above analysis. This means that different driving forces must be employed for vapor diffusion and liquid transport. The choice of temperature and relative humidity as driving potentials offers particular advantages. Vapor pressure, as the driving force for diffusion, is uniquely determined by the two quantities. The two potentials are continuous across the building component, i.e. there are no discontinuities at material interfaces, as would be the case with water content. In addition, the hygrothermal material properties and boundary conditions discussed in the following can easily be defined in terms of these quantities.

Hygrothermal Material Properties

The results of a computer simulation are only as good as the employed material parameters. Since the notorious lack of reliable material data has been a longstanding obstacle for the acceptance of modern calculation methods, it will be discussed in the following which parameters are actually needed for different kinds of investigations. In general, the following material properties are necessary for the non-steady computation of the temperature fields:

• Bulk density Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho} of the dry material
• specific heat capacity Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c}
• thermal conductivity Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda}

If the effect of moisture in the material on the U-factor is to be quantified, the thermal conductivity must be entered as a function of moisture content, cf. Fig. 1. Relevant data can be found in [1] or in WUFI's material database. On the other hand, if the investigation concerns mainly the hygric behavior of the component, then it is sufficient to use the design value Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_R} which already allows for the practical moisture content of the respective material. That is, in most cases all necessary thermal properties can be found in German standard DIN 4108-4 or in the respective certificates of approval.

The hygric properties that need to be known for all (i.e. also for non-hygroscopic) materials are:

• Water vapor diffusion resistance factor µ (µ-value)
• Porosity Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon} (as a measure of the maximum possible water content wmax)

The µ-values for a large number of building materials can also be found in DIN 4108-4. The porosity can be determined from bulk density and true density or from the maximum water saturation. It only applies if the material can take up water or water vapor in its pore spaces. The material data mentioned so far, however, only allow simulations without sorption or liquid transport effects, i.e. a kind of non-steady Glaser calculation.

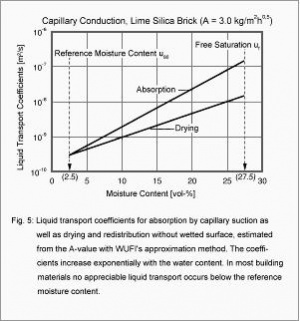
If the behavior of hygroscopic, capillary active materials is to be simulated correctly, the moisture storage function shown in Fig. 3 and the moisture-dependent liquid transport coefficients shown in Fig. 5 are also needed. For these coefficients the process-specific differentiation shown in the figure has proved advantageous. The reason is that the capillary absorption of water by mineral materials in contact with water is a much faster process than the capillary redistribution or the drying process after the water supply has been cut off.

For numerous building materials these additional parameters which describe the hygroscopic and the capillary properties are now available from relevant databases (such as the WUFI database). Measuring the moisture storage function and the liquid transport coefficients is somewhat costly and laborious [6], so that it is usually not feasible for the practitioner. In many cases, however, approximation methods can be used to estimate the material properties from known data. For example, if the capillary active material layers in a component are not in direct contact with each other, or if this contact interface does not become wet for prolonged periods of time (i.e. no appreciable capillary exchange of water occurs across the interface), then sufficiently accurate calculation results can be obtained by estimating the moisture storage function from the reference moisture content u80 (equilibrium moisture at 80% RH, in accordance with DIN 52620) and the free saturation uf by means of the approximation method implemented in WUFI [2].

Similarly, the liquid transport coefficients (Fig. 5) may be estimated from the A-value (the water absorption coefficient as defined in DIN 52617) by a method which is also integrated in WUFI.

In this way hygroscopic and capillary active materials can be specified accurately enough for most practical applications by means of the following material parameters (in addition to the standard parameters in DIN 4108-4):

• reference moisture content u80
• free water saturation uf
• water absorption coefficient (A-value)

The free water saturation is the moisture content which can be determined from the wetted-through specimen in the course of a measurement of the A-value.

Since all properties of building materials are subject to variations due to the manufacturing process or different standards of workmanship, it is useful to perform variations of the parameters in the calculations within certain intervals - in analogy to the span of parameters given in DIN 4108-4 - and to document the effect of these variations on the calculation results. If the effect of a material parameter turns out to be negligible in the application case at hand, then it need not be determined exactly. On the other hand, if the effect of the parameter is decisive for the interpretation of the results, then standard or literature data may be inadequate and precise measurements of the parameter may be required.

Climate and Surface Transfer Conditions

Via its surfaces, every building component is undergoing hygrothermal interaction with its surroundings. That is, the surroundings are affecting the component and the component is affecting its surroundings, for example by releasing stored heat or by sorptive buffering of indoor air humidity. This fact has to be allowed for when boundary conditions are specified. Basically, three types of boundary conditions must be distinguished: the exterior ambient conditions above and below the ground, and the indoor conditions. In all three cases, different surface transfer conditions have to be employed, due to the different exchange processes involving convection and radiation or conduction and diffusion.

Exterior Climate

The exterior climate conditions acting on the component are air temperature, relative humidity, solar radiation and precipitation. The radiation and precipitation loads depend on the inclination and orientation of the component and must accordingly be computed for the specific component. In addition, wind speed and direction as well as the exposition of the building to wind flow and local wind flow patterns need to be known for determining driving rain. If long-wave emission is to be allowed for, too, data on ground and air counterradiation are also needed.

The daily variation of the climate conditions - the variation of the exterior air temperature is illustrated in Fig. 6 - usually requires sufficiently short time steps. For hygrothermal simulations hourly values have proved suitable [7]. For example, hourly climate data are available in the form of the German Test Reference Years (TRY) of the Deutscher Wetterdienst which contain average climate conditions for 12 different regions of the former West Germany. However, moisture problems usually occur under extreme climate conditions rather than average conditions. Depending on the case at hand, the worst moisture conditions may result from a particularly cold year (e.g. interstitial condensation in winter) or from a particularly warm year (e.g. summer condensation) [8]. For this reason, two meteorological data sets have been selected from the extensive collection of weather data measured in Holzkirchen which represent the statistically warmest and coldest year in a period of ten years, respectively. These Hygrothermal Reference Years (HRY) will be offered for free download.

Hygrothermal Conditions Below Ground

Below ground, the variations of the exterior air temperature only propagate strongly damped. Fig. 6 shows the temperatures measured for the year 1999 at a depth of 1 m below the surface and compares them to the exterior air temperatures. At this depth the damping has already eliminated all daily variations. Furthermore, there is a phase shift of several weeks with respect to the air temperature which is most noticeable in spring and in autumn. The measured data include the effect of precipitation (rain water or melted snow seeping into the ground etc.). Since the measurements are being performed at some distance from the nearest buildings, the temperatures are lower than they would be close to a building which releases heat into the ground. The humidity in the ground usually lies between 99% and 100% RH if vegetation is present, since plants cannot extract moisture from the ground at lower humidities. This also applies to substrate layers in planted roofs, although at different temperature levels.

Interior Climate

The interior climate conditions specified in DIN 4108-3 for the dew period (20°C, 50% RH) and for the evaporation period (12°C, 70% RH) have proved suitable for the general assessment of diffusion processes in building components, but they do not represent realistic boundary conditions for a simulation spanning a year.

Measurements in residential dwellings [9] show that the monthly indoor moisture load (i.e. the difference between the moisture contents of the indoor and the outdoor air) decreases almost linearly with the exterior temperature. This is due to the occupants keeping the windows open more often during the warmer seasons. Depending on the habits of the occupants and the airtightness of the building, the moisture load in winter (at 0°C) lies between 2 g/m³ und 6 g/m³. Under a normal moisture load (4 g/m³) the average German exterior climate conditions result in the indoor air temperatures and humidities shown in Fig. 7. This typical indoor climate is representative for the conditions in living quarters including kitchen and bathroom. It already contains a certain safety margin, in particular if rooms with low moisture load, such as offices or bedrooms, are under investigation. Use of this climate is therefore appropriate if no further details are known about the interior climate and no measured data are available.

Surface Transfer Conditions

The exterior climate (except the situation below ground) as well as the interior climate affect the component surface, with a boundary air layer right at the surface acting as an intermediary. This boundary layer represents a wind-dependent resistance for heat and moisture transport which is quantified by the respective surface transfer coefficients. In general, detailed modeling of the specific effects of convection and its flow patterns at the component is not necessary since the transfer resistances are small compared to the resistances of the individual material layers. Therefore the average values for the exterior and interior heat and vapor transfer cofficients listed in table 1 are sufficient for most applications.

Table 1: Average surface transfer coefficients for calculating the heat and moisture exchange between exterior or interior component surfaces and the environment

The heat transfer coefficients contain a component which describes long-wave radiation exchange. This is only valid, however, as long as the convective and the radiative heat flows go in the same direction. When the surface temperature of a highly insulated component falls below the ambient air temperature by night due to radiative cooling, this is no longer the case. Computer simulations of nighttime condensation on such components therefore require a suitable correction of the surface transfer coefficients or compensation by empirically adapting the long-wave emissivity, based on comparison with experimental results.

The effects of solar radiation and precipitation on the component are best described by heat and moisture sources. An energy absorption factor which depends on the surface color allows for the fact that only part of the short-wave radiation incident on the component is converted into heat. This absorption factor is ca. 0.4 for bright surfaces, such as white exterior renderings, and between 0.6 and 0.8 for dark surfaces, such as painted wood, clinker, roofing tiles and bituminous sheeting. An absorption factor may also be employed for driving rain, since only part of the incident rain water stays at the surface and can be absorbed. The rest splashes off on hitting the facade or runs off due to gravity. Experience shows that 0.7 usually is an appropriate value for the rain water absorption factor of vertical surfaces.

The Calculation Model

A number of hygrothermal simulation models which provide reliable results has been developed in different countries [10]. The following description discusses the model which forms the basis for the PC program WUFI (Wärme- Und Feuchtetransport Instationär) [2]. In this model the non-steady heat amd moisture transport processes in building components are described by the following coupled differential equations:

The left-hand sides of both equations consist of the storage terms. Heat storage comprises the heat capacity of the dry material and the heat capacity of the moisture present in the material. Moisture storage is described by the derivative of the moisture storage function mentioned above. On the righ-hand side of the equations we find the transport terms. Heat transport is the sum of moisture-dependent thermal conductivity and vapor enthalpy flow. This heat transport by vapor enthalpy flow is due to water evaporating in one place and thereby absorbing latent heat from this place, and then diffusing to a different place, condensing there and releasing latent heat. This kind of heat transport is often called latent heat effect.

Liquid transport (through surface diffusion and capillary conduction, both due to a gradient of relative humidity) shows only a relatively minor temperature dependence. Vapor diffusion, on the other hand, is strongly affected by the temperature field, since the saturation vapor pressure increases exponentially with temperature.

The differential equations are discretised by means of an implicit finite volume method and are iteratively solved according to the scheme described by the flow chart shown in Fig. 8. The accuracy of the numerical solution depends on the mesh widths of the numerical grid, the size of the time steps and the choice of the convergence criteria. Usually the numerical solution is sufficiently accurate, so that the effect of numerical parameters can be ignored in comparison with the effects of the physical parameters like material and climate data. After the calculation the result should be critically assessed in order to exclude user errors or severe convergence errors. Convergence errors are indicated by WUFI, and their effect is assessed by a comparison of the sum of the moisture flows with the water accumulated in the component. False input or unrealistic material data can only be controlled by plausibility checks.