Details:MoistureStorageFunction
Moisture Storage Function
The moisture storage function
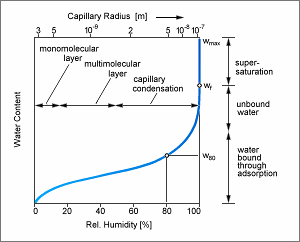
In a porous hygroscopic material, the surfaces of the pore system accumulate water molecules until a specific equilibrium moisture content corresponding to the humidity of the ambient air is reached. Due to the reduction of the saturation vapor pressure in the smaller capillaries, there is also some condensation which - at relative humidities above ca. 0.6 .. 0.8 - results in a marked increase of the equilibrium moisture.
A capillary-active material in contact with water will take up this water until it reaches its free saturation wf. This water content wf corresponds to the moisture storage function at a relative humidity of 1 (=100%). Because of air pockets trapped in the pore structure, however, the free saturation is less than the maximum water content wmax which is determined by the porosity. Moisture contents exceeding wf may e.g. result from condensation in a temperature gradient (especially in insulation materials; these are often not capillary-active and therefore have wf ~ 0).
The free saturation wf ranks among the standard material data and is known for most materials. The 'practical moisture content' w80 that corresponds to the equilibrium moisture at a RH of 0.8 is another standard quantity.
The dependence of the moisture storage function on the temperature is marginal and is ignored in WUFI.
Measurement of the moisture storage function
Because of limitations of the respective measuring procedures, the moisture storage function has to be composed from sorption isotherms (up to ~ 0.9 RH) and pressure plate measurements (above 0.95 RH) [1]. The hysteresis between adsorption and desorption isotherms is usually not very pronounced, so that it is sufficient to use the adsorption isotherm. Where necessary, a mean isotherm may be used. Due to the measuring technique, the pressure plate measurements are 'desorption' measurements.
The moisture storage function in WUFI
In WUFI, the moisture storage function is described by means of a table with relative humidities and the corresponding moisture contents. The table may contain an arbitrary number of entries between which WUFI interpolates linearly.
Example: Sander sandstone
| j [-] | w[kg/m³] |
| 0 | 0 |
| 0.1 | 4.4 |
| 0.3 | 10.2 |
| 0.65 | 15.2 |
| 0.8 | 19.0 |
| 0.91 | 30.0 |
| 0.95 | 45.9 |
| 0.99 | 61.7 |
| 0.995 | 75.0 |
| 1.0 | 130.0 |
The pressure plate measurements would even allow a still finer subdivision of the table in the high-moisture region, but then at φ ~ 1 the curve would approach the ordinate so closely that its immensely steep slope might cause numerical problems. If the moisture transport across the interface between two capillary-active materials in capillary contact is to be calculated, however, the moisture storage function must be as detailed as possible in this region [2]. (If the capillary contact is non-ideal, an additional transfer resistance has to be taken into account [2]).
WUFI allows moisture contents in the supersaturated region, since
these may well occur under condensation conditions. However, in
this region there is no unique functional relation between relative
humidity and moisture content. The relative humidity is always 1,
and the moisture content varies between wf and
wmax.
The moisture content thus doesn't depend on the relative humidity,
it is determined by the boundary conditions: it increases under
condensation conditions and decreases under evaporation conditions.
In order to treat these moisture contents above wf,
WUFI internally extends the table of each material by introducing
an additional entry:
| φ[-] | w[kg/m³] |
| ... | ... |
| 1.01 | wmax |
Relative humidities between 1 and 1.01 are only fictitious, of course, but they allow WUFI to assign a unique RH to each water content, as required by the moisture transport equations.
During the calculation WUFI performs iterations where it samples small regions of the tabulated curve. Very sharp bends in the curve may throw the iteration off and thus impede its convergence. In such a case, the curve should be smoothed by inserting additional points. A large number of entries may slow the search in the table, however.
Approximation of the moisture storage function
If the moisture storage function can be adequately described by the function
| w = wf· | (b-1)·φ b-φ | |
| w | [kg/m³]: | moisture content corresponding to relative humidity φ |
| wf | [kg/m³]: | moisture content at free saturation |
| φ | [-]: | relative humidity |
| b | [-]: | approximation factor, |
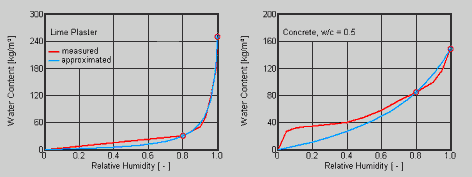
then it is sufficient to specify w80 and wf, in order to define the moisture storage function for WUFI (this is called 'approximation of the moisture storage function'). However, this condition is not met by all materials (e.g. some kinds of concrete).
WUFI's default moisture storage function
The moisture storage function of non-hygroscopic materials
(essentially insulating materials, but
air layers as well) is
theoretically more or less zero in the region
φ = 0..1, whereas for
φ = 1 it takes on some indefinite
value between zero and wmax, so that no
well-defined functional relationship exists. Because of numerical
requirements, however, WUFI assigns a (low) artificial moisture
storage function to all materials for which the user did not
define such a function.
So the results of a WUFI calculation will indicate some (low)
moisture content even in materials for which you did not define
a moisture storage function. These moisture contents are artificial
and should be regarded with caution. Only when the moisture contents
surpass the fictitious free saturation of ca. 0.05·wmax,
they have resulted from condensation phenomena which are independent
from the choice of the moisture storage function. In that case the
excess of the moisture content over wf can with
appropriate caution be regarded as a realistic measure of the
amount of condensed moisture.
For discussion of some specific questions concerning the moisture storage function, see the Questions & Answers section.
Literature:
| [1] | Krus, M.: Moisture Transport and
Storage Coefficients of Porous Mineral Building Materials.
Theoretical Principles and New Test Methods |
| [2] | Holm, A., Krus, M., Künzel, H.M.:
Feuchtetransport über Materialgrenzen im Mauerwerk. |